The Affine Heat Method
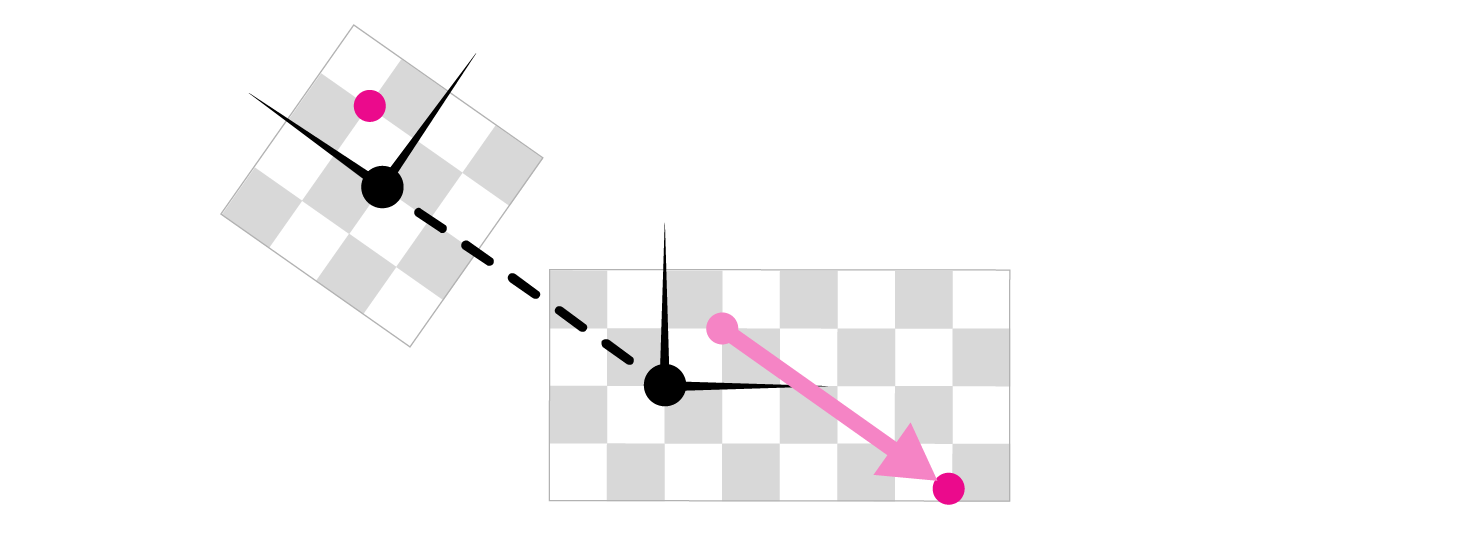
Riemannian logarithmic maps, or geodesic polar coordinates, can be computed via parallel transport along minimal geodesics with respect to a connection modeled on Euclidean transformations. The discretization of this connection is given by parallel transport maps that align neighboring tangent spaces with the discrete Levi-Civita connection followed up with a translation in the direction of the edge vector.
This work presents the Affine Heat Method for computing logarithmic maps.
These maps are local surface parameterizations defined by the direction and distance along shortest geodesic paths from a given source point, and arise in many geometric tasks from local texture mapping to geodesic distance-based optimization.
Our main insight is to define a connection Laplacian with a homogeneous coordinate accounting for the translation between tangent coordinate frames; the action of short-time heat flow under this Laplacian gives both the direction and distance from the source, along shortest geodesics.
The resulting numerical method is straightforward to implement, fast, and improves accuracy compared to past approaches.
We present two variants of the method, one of which enables pre-computation for fast repeated solves, while the other resolves the map even near the cut locus in high detail.
As with prior heat methods, our approach can be applied in any dimension and to any spatial discretization, including polygonal meshes and point clouds, which we demonstrate along with applications of the method.